JavaScript Algorithms and Data Structures 源码分析(13) -- 红黑树 red-black-tree

红黑树

红黑树是一种自平衡的二叉搜索树，在计算机科学中使用。二叉树的每个节点都有一个额外的位，这个位通常被解释为节点的颜色（红色或黑色）。这些颜色位用于在插入和删除过程中保持树的大致平衡。

通过以一种满足特定属性的方式将树的每个节点标记为两种颜色之一，可以保持树的平衡，这些属性共同限制了树在最坏情况下可能变得不平衡的程度。当修改树时，新的树会被重新排列和重新标记以恢复颜色属性。这些属性的设计使得这种重新排列和重新标记可以高效地进行。

树的平衡并不完美，但足够好，可以确保在 O(log n)的时间内进行搜索，其中 n 是树中的元素总数。插入和删除操作以及树的重新排列和重新标记也可以在 O(log n)的时间内完成。

红黑树的一个示例：

属性

除了对二叉搜索树施加的要求之外，红黑树还必须满足以下条件：

• 每个节点要么是红色，要么是黑色。
• 根节点是黑色。这个规则有时可以省略。因为根节点总是可以从红色变为黑色，但不一定反之，所以这个规则对分析的影响很小。
• 所有叶子节点（NIL）都是黑色的。
• 如果一个节点是红色的，则它的两个子节点都是黑色的。
• 从给定节点到任何其后代 NIL 节点的每条路径都包含相同数量的黑色节点。

一些定义：从根节点到一个节点的黑色节点数称为该节点的黑色深度；从根节点到叶子节点的所有路径中的黑色节点数是红黑树的黑色高度。

这些约束条件强制实施了红黑树的一个关键特性：从根节点到最远叶子节点的路径长度不超过从根节点到最近叶子节点路径长度的两倍。结果是树大致上是高度平衡的。由于插入、删除和查找值等操作的最坏情况时间与树的高度成比例，这个对树高度的理论上限使得红黑树在最坏情况下具有高效性，而普通的二叉搜索树则不具备。

插入平衡

If uncle is RED

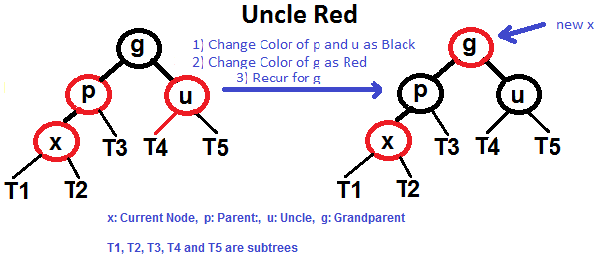
If uncle is BLACK

• 左左情况（p 是 g 的左子节点，x 是 p 的左子节点）
• 左右情况（p 是 g 的左子节点，x 是 p 的右子节点）
• 右右情况（p 是 g 的右子节点，x 是 p 的右子节点）
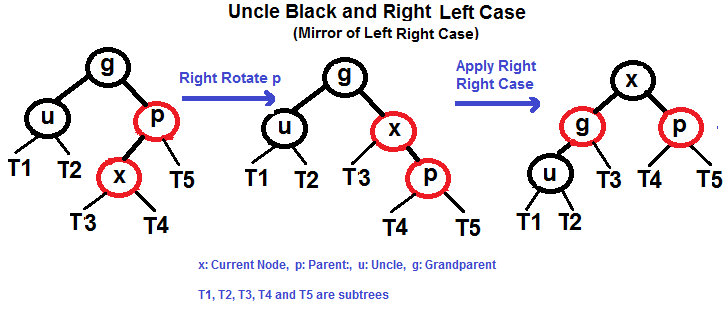
• 右左情况（p 是 g 的右子节点，x 是 p 的左子节点）

Left Left Case (See g, p and x)

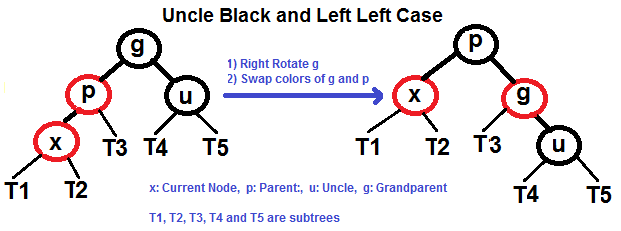
Left Right Case (See g, p and x)

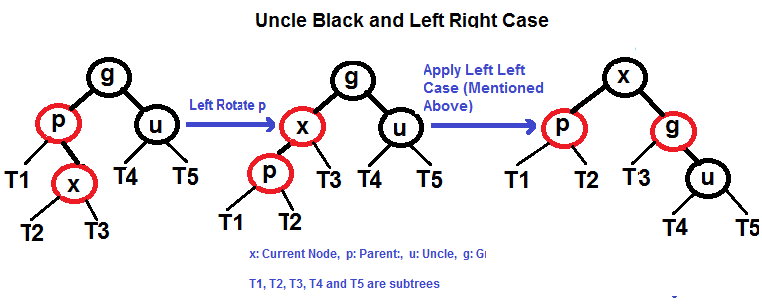
Right Right Case (See g, p and x)

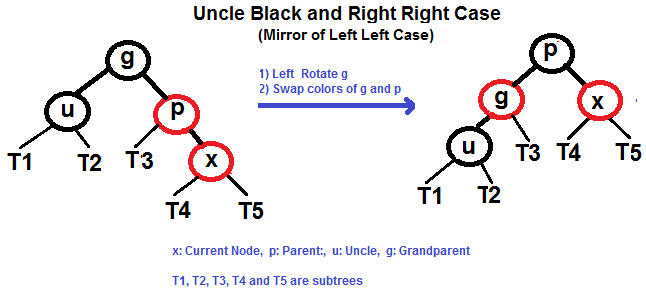
Right Left Case (See g, p and x)

RedBlackTree

// 红黑树节点的可能颜色。
const RED_BLACK_TREE_COLORS = {
  red: "red",
  black: "black",
};

// 节点的元信息中颜色熟悉名称
const COLOR_PROP_NAME = "color";

export default class RedBlackTree extends BinarySearchTree {
  /**
   * @param {*} value
   * @return {BinarySearchTreeNode}
   */
  insert(value) {
    // 将值插入，并获取插入的节点。
    const insertedNode = super.insert(value);

    // 检查插入的节点是否为树的根节点。
    if (this.nodeComparator.equal(insertedNode, this.root)) {
      // 如果插入的节点是根节点，则将其设置为黑色，以满足红黑树的性质。
      this.makeNodeBlack(insertedNode);
    } else {
      // 如果插入的节点不是根节点，则将其设置为红色，以便进行平衡。
      this.makeNodeRed(insertedNode);
    }

    // 通过检查条件并执行必要的旋转操作来平衡树。
    this.balance(insertedNode);
    // 返回插入的节点。
    return insertedNode;
  }

  /**
   * @param {*} value
   * @return {boolean}
   */
  remove(value) {
    throw new Error(`Can't remove ${value}. Remove method is not implemented yet`);
  }

  /**
   * 平衡红黑树的方法
   * @param {BinarySearchTreeNode} node
   */
  balance(node) {
    // 如果节点是根节点，则不需要平衡
    if (this.nodeComparator.equal(node, this.root)) {
      return;
    }

    // 如果父节点是黑色，则不需要平衡
    if (this.isNodeBlack(node.parent)) {
      return;
    }

    const grandParent = node.parent.parent;

    if (node.uncle && this.isNodeRed(node.uncle)) {
      // 如果节点有红色的叔叔节点，需要进行重新着色

      // 将父节点和叔叔节点设置为黑色
      this.makeNodeBlack(node.uncle);
      this.makeNodeBlack(node.parent);

      if (!this.nodeComparator.equal(grandParent, this.root)) {
        // 如果祖父节点不是根节点，则将其重新着色为红色
        this.makeNodeRed(grandParent);
      } else {
        // 如果祖父节点是黑色的根节点，则不需要进行其他操作
        // 因为根节点已经有两个黑色的兄弟节点了，我们刚刚重新着色了它们
        return;
      }

      // 现在需要进一步检查重新着色后的祖父节点
      this.balance(grandParent);
    } else if (!node.uncle || this.isNodeBlack(node.uncle)) {
      // 如果节点的叔叔节点是黑色或不存在，则需要进行旋转操作

      if (grandParent) {
        // 旋转后将得到的新的祖父节点
        let newGrandParent;

        if (this.nodeComparator.equal(grandParent.left, node.parent)) {
          // 左侧情况
          if (this.nodeComparator.equal(node.parent.left, node)) {
            // 左-左情况
            newGrandParent = this.leftLeftRotation(grandParent);
          } else {
            // 左-右情况
            newGrandParent = this.leftRightRotation(grandParent);
          }
        } else {
          // 右侧情况
          if (this.nodeComparator.equal(node.parent.right, node)) {
            // 右-右情况
            newGrandParent = this.rightRightRotation(grandParent);
          } else {
            // 右-左情况
            newGrandParent = this.rightLeftRotation(grandParent);
          }
        }

        // 如果新的祖父节点没有父节点，则将其设置为根节点
        if (newGrandParent && newGrandParent.parent === null) {
          this.root = newGrandParent;

          // 将根节点重新着色为黑色
          this.makeNodeBlack(this.root);
        }

        // 检查新的祖父节点是否违反了红黑树的规则
        this.balance(newGrandParent);
      }
    }
  }

  /**
   * 左左情况（p是g的左子节点且x是p的左子节点）
   * @param {BinarySearchTreeNode|BinaryTreeNode} grandParentNode
   * @return {BinarySearchTreeNode}
   */
  leftLeftRotation(grandParentNode) {
    // 记录祖父节点的父节点。
    const grandGrandParent = grandParentNode.parent;

    // 检查祖父节点是否是祖父父节点的左子节点。
    let grandParentNodeIsLeft;
    if (grandGrandParent) {
      grandParentNodeIsLeft = this.nodeComparator.equal(grandGrandParent.left, grandParentNode);
    }

    // 记录祖父节点的左子节点。
    const parentNode = grandParentNode.left;

    // 记录父节点的右子节点，因为我们将把它转移到祖父节点的左子树中。
    const parentRightNode = parentNode.right;

    // 将祖父节点设置为父节点的右子节点。
    parentNode.setRight(grandParentNode);

    // 将父节点的右子树移到祖父节点的左子树中。
    grandParentNode.setLeft(parentRightNode);

    // 将父节点放在祖父节点的位置。
    if (grandGrandParent) {
      if (grandParentNodeIsLeft) {
        grandGrandParent.setLeft(parentNode);
      } else {
        grandGrandParent.setRight(parentNode);
      }
    } else {
      // 将父节点设置为根节点。
      parentNode.parent = null;
    }

    // 交换祖父节点和父节点的颜色。
    this.swapNodeColors(parentNode, grandParentNode);

    // 返回新的根节点。
    return parentNode;
  }

  /**
   * 执行左-右旋转，即对给定的祖父节点进行旋转操作。
   * @param {BinarySearchTreeNode|BinaryTreeNode} grandParentNode - 祖父节点。
   * @return {BinarySearchTreeNode} - 旋转后的根节点。
   */
  leftRightRotation(grandParentNode) {
    // 存储父节点和子节点的引用。
    const parentNode = grandParentNode.left;
    const childNode = parentNode.right;

    // 存储子节点的左子节点，以保留左子树。
    const childLeftNode = childNode.left;

    // 将父节点设为子节点的左子节点。
    childNode.setLeft(parentNode);

    // 将子节点的左子树移到父节点的右子树中。
    parentNode.setRight(childLeftNode);

    // 将左-右子节点放置在祖父节点的左子节点位置。
    grandParentNode.setLeft(childNode);

    // 现在可以执行左-左旋转了。
    return this.leftLeftRotation(grandParentNode);
  }

  /**
   * 右右旋转情况（p是g的右子节点，x是p的右子节点）
   * @param {BinarySearchTreeNode|BinaryTreeNode} grandParentNode
   * @return {BinarySearchTreeNode}
   */
  rightRightRotation(grandParentNode) {
    // 记录祖父节点的父节点
    const grandGrandParent = grandParentNode.parent;

    // 检查祖父节点是左子节点还是右子节点
    let grandParentNodeIsLeft;
    if (grandGrandParent) {
      grandParentNodeIsLeft = this.nodeComparator.equal(grandGrandParent.left, grandParentNode);
    }

    // 记录祖父节点的右子节点
    const parentNode = grandParentNode.right;

    // 记录父节点的左子节点，因为我们将它移动到爷爷节点的右子树中
    const parentLeftNode = parentNode.left;

    // 将爷爷节点作为父节点的左子节点
    parentNode.setLeft(grandParentNode);

    // 将父节点的左子节点转移到爷爷节点的右子树中
    grandParentNode.setRight(parentLeftNode);

    // 将父节点放在爷爷节点的位置
    if (grandGrandParent) {
      if (grandParentNodeIsLeft) {
        grandGrandParent.setLeft(parentNode);
      } else {
        grandGrandParent.setRight(parentNode);
      }
    } else {
      // 将父节点设为根节点
      parentNode.parent = null;
    }

    // 交换父节点和爷爷节点的颜色
    this.swapNodeColors(parentNode, grandParentNode);

    // 返回新的根节点
    return parentNode;
  }

  /**
   * 对给定的祖父节点执行右-左旋转。
   * @param {BinarySearchTreeNode|BinaryTreeNode} grandParentNode
   * @return {BinarySearchTreeNode}
   */
  rightLeftRotation(grandParentNode) {
    // 记住父节点和父节点的左子节点。
    const parentNode = grandParentNode.right;
    const childNode = parentNode.left;

    // 记住左子节点的右子节点，以防丢失右子树。稍后将重新分配给父节点的左子树。
    const childRightNode = childNode.right;

    // 将父节点设为左子节点的右子节点。
    childNode.setRight(parentNode);

    // 将左子节点的右子树移动到父节点的左子树。
    parentNode.setLeft(childRightNode);

    // 将左子节点放在祖父节点的右子节点的位置。
    grandParentNode.setRight(childNode);

    // 现在可以执行右-右旋转了。
    return this.rightRightRotation(grandParentNode);
  }

  /**
   * @param {BinarySearchTreeNode|BinaryTreeNode} node
   * @return {BinarySearchTreeNode}
   */
  makeNodeRed(node) {
    node.meta.set(COLOR_PROP_NAME, RED_BLACK_TREE_COLORS.red);

    return node;
  }

  /**
   * @param {BinarySearchTreeNode|BinaryTreeNode} node
   * @return {BinarySearchTreeNode}
   */
  makeNodeBlack(node) {
    node.meta.set(COLOR_PROP_NAME, RED_BLACK_TREE_COLORS.black);

    return node;
  }

  /**
   * @param {BinarySearchTreeNode|BinaryTreeNode} node
   * @return {boolean}
   */
  isNodeRed(node) {
    return node.meta.get(COLOR_PROP_NAME) === RED_BLACK_TREE_COLORS.red;
  }

  /**
   * @param {BinarySearchTreeNode|BinaryTreeNode} node
   * @return {boolean}
   */
  isNodeBlack(node) {
    return node.meta.get(COLOR_PROP_NAME) === RED_BLACK_TREE_COLORS.black;
  }

  /**
   * @param {BinarySearchTreeNode|BinaryTreeNode} node
   * @return {boolean}
   */
  isNodeColored(node) {
    return this.isNodeRed(node) || this.isNodeBlack(node);
  }

  /**
   * @param {BinarySearchTreeNode|BinaryTreeNode} firstNode
   * @param {BinarySearchTreeNode|BinaryTreeNode} secondNode
   */
  swapNodeColors(firstNode, secondNode) {
    const firstColor = firstNode.meta.get(COLOR_PROP_NAME);
    const secondColor = secondNode.meta.get(COLOR_PROP_NAME);

    firstNode.meta.set(COLOR_PROP_NAME, secondColor);
    secondNode.meta.set(COLOR_PROP_NAME, firstColor);
  }
}