JavaScript Algorithms and Data Structures 源码分析(11) -- 二叉搜索树 binary-search-tree

发表于 分类于 阅读次数： 本文字数： 1.5k 阅读时长 ≈ 5 分钟

二叉搜索树

二叉搜索树（Binary Search Tree，简称 BST）是计算机科学中一种特定类型的容器，有时也被称为有序二叉树或排序二叉树。它们用于在内存中存储“项”（如数字、名称等），可以快速进行查找、添加和删除操作。它们可以用于实现动态集合或查找表，以便通过键来查找项（例如，通过姓名查找人的电话号码）。

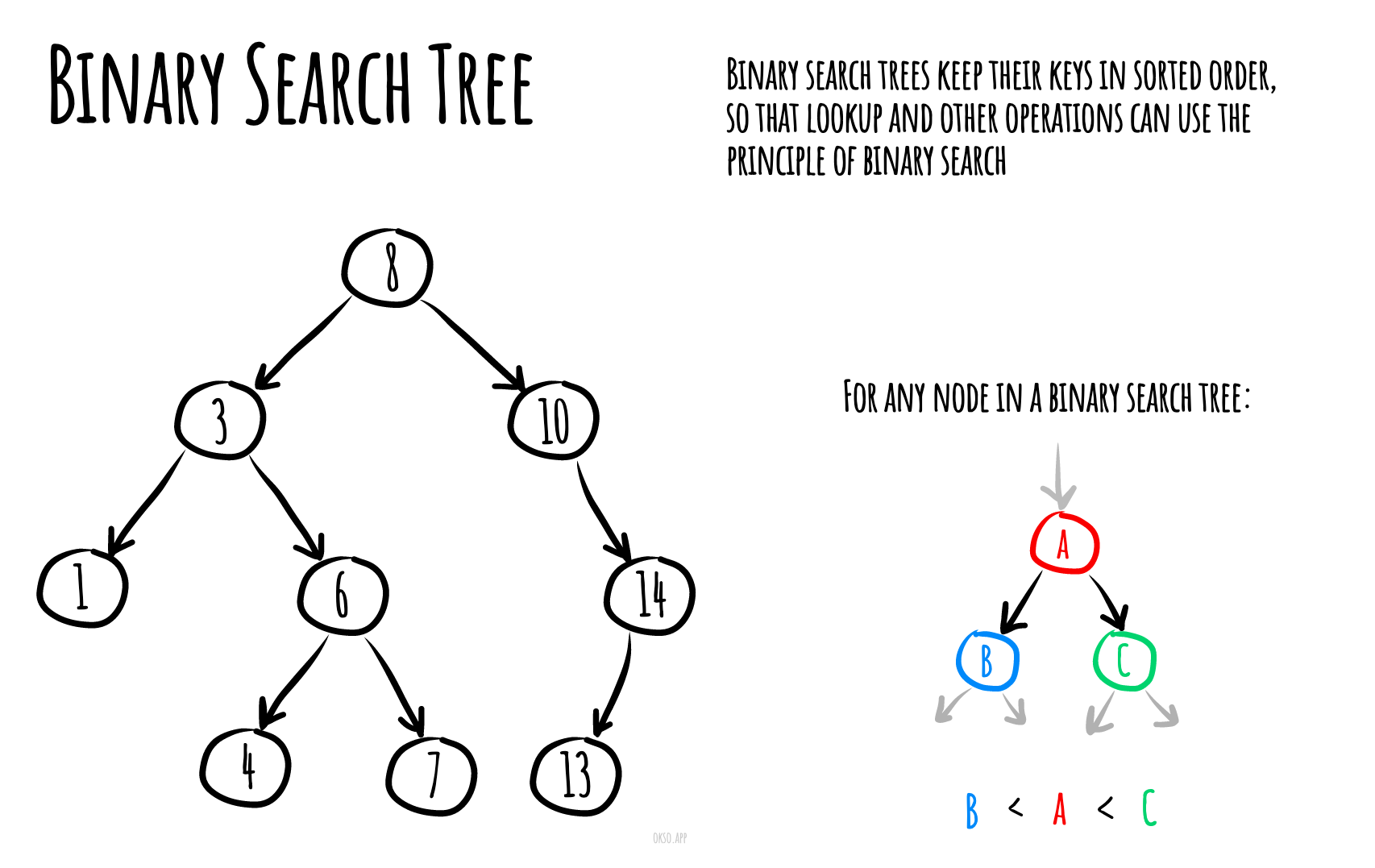
二叉搜索树将其键按照排序顺序存储，以便查找和其他操作可以使用二分查找的原理：在树中查找键（或查找要插入新键的位置）时，从根到叶子遍历树，与树节点中存储的键进行比较，并根据比较结果决定是继续在左子树还是右子树中搜索。平均而言，这意味着每次比较都可以跳过树的约一半，因此每次查找、插入或删除操作的时间与树中存储的项数的对数成比例。这比在（未排序的）数组中按键查找项所需的线性时间要好得多，但比哈希表上的相应操作要慢。

下图是一个大小为 9、深度为 3 的二叉搜索树示例，根节点为 8。叶子节点未绘制。

binary-search-tree

BinarySearchTreeNode

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
export default class BinarySearchTreeNode extends BinaryTreeNode {
  /**
   * @param {*} [value] - node value.
   * @param {function} [compareFunction] - comparator function for node values.
   */
  // 定义 BinarySearchTreeNode 类的构造函数。
  // 它接受一个可选的 value 参数和一个可选的 compareFunction 参数。
  constructor(value = null, compareFunction = undefined) {
    // 使用 value 参数调用父类 BinaryTreeNode 的构造函数。
    super(value);

    // This comparator is used to compare node values with each other.
    // 将 compareFunction 参数赋值给实例的 compareFunction 属性。
    this.compareFunction = compareFunction;

    // 创建 Comparator 类的新实例，并将其赋值给实例的 nodeValueComparator 属性。
    // 将 compareFunction 参数传递给 Comparator 构造函数。
    this.nodeValueComparator = new Comparator(compareFunction);
  }

  /**
   * 将一个值插入到二叉搜索树中。
   * @param {*} value - 要插入的值。
   * @return {BinarySearchTreeNode} - 插入的节点。
   */
  insert(value) {
    // 如果当前节点为空，将值设置为当前节点的值。
    if (this.nodeValueComparator.equal(this.value, null)) {
      this.value = value;

      return this;
    }

    // 如果要插入的值小于当前节点的值，进入左子树。
    if (this.nodeValueComparator.lessThan(value, this.value)) {
      // 如果存在左子节点，递归调用插入方法。
      if (this.left) {
        return this.left.insert(value);
      }

      // 如果不存在左子节点，创建一个新节点并将其设置为左子节点。
      const newNode = new BinarySearchTreeNode(value, this.compareFunction);
      this.setLeft(newNode);

      return newNode;
    }

    // 如果要插入的值大于当前节点的值，进入右子树。
    if (this.nodeValueComparator.greaterThan(value, this.value)) {
      // 如果存在右子节点，递归调用插入方法。
      if (this.right) {
        return this.right.insert(value);
      }

      // 如果不存在右子节点，创建一个新节点并将其设置为右子节点。
      const newNode = new BinarySearchTreeNode(value, this.compareFunction);
      this.setRight(newNode);

      return newNode;
    }

    // 如果要插入的值等于当前节点的值，返回当前节点。
    return this;
  }

  /**
   * 在二叉搜索树中查找具有给定值的节点。
   * @param {*} value - 要查找的值。
   * @return {BinarySearchTreeNode} - 具有给定值的节点，如果未找到则返回null。
   */
  find(value) {
    // 检查当前节点是否具有目标值。
    if (this.nodeValueComparator.equal(this.value, value)) {
      return this;
    }

    // 如果目标值小于当前节点的值并且存在左节点，在左子树中递归搜索目标值。
    if (this.nodeValueComparator.lessThan(value, this.value) && this.left) {
      // Check left nodes.
      return this.left.find(value);
    }

    // 如果目标值大于当前节点的值并且存在右节点，在右子树中递归搜索目标值。
    if (this.nodeValueComparator.greaterThan(value, this.value) && this.right) {
      // Check right nodes.
      return this.right.find(value);
    }

    // 在树中未找到目标值。
    return null;
  }

  /**
   * @param {*} value
   * @return {boolean}
   */
  contains(value) {
    return !!this.find(value);
  }

  /**
   * 从二叉搜索树中移除具有特定值的节点。
   * @param {*} value - 要移除的节点的值。
   * @return {boolean} - 如果成功移除节点，则返回true；否则返回false。
   */
  remove(value) {
    // 找到要移除的节点。
    const nodeToRemove = this.find(value);

    // 如果未找到节点，则抛出错误。
    if (!nodeToRemove) {
      throw new Error("Item not found in the tree");
    }
    // 获取节点的父节点。
    const { parent } = nodeToRemove;
    // 如果节点是叶子节点（没有子节点）。
    if (!nodeToRemove.left && !nodeToRemove.right) {
      // 如果节点有父节点，则从父节点中移除对该节点的引用。
      if (parent) {
        parent.removeChild(nodeToRemove);
      } else {
        // 否则，只需将当前节点的值设置为undefined。
        nodeToRemove.setValue(undefined);
      }
    } else if (nodeToRemove.left && nodeToRemove.right) {
      // 如果节点有两个子节点。
      // 找到比要移除的节点值更大的下一个节点（右侧分支中的最小值）。
      const nextBiggerNode = nodeToRemove.right.findMin();
      // 如果下一个更大的节点不是要移除节点的右子节点，
      // 则移除下一个更大的节点，并将要移除的节点的值替换为该节点的值。
      if (!this.nodeComparator.equal(nextBiggerNode, nodeToRemove.right)) {
        this.remove(nextBiggerNode.value);
        nodeToRemove.setValue(nextBiggerNode.value);
      } else {
        // 否则，如果下一个右侧节点是下一个更大的节点，并且它没有左子节点，
        // 则只需用右侧节点替换要删除的节点。
        nodeToRemove.setValue(nodeToRemove.right.value);
        nodeToRemove.setRight(nodeToRemove.right.right);
      }
    } else {
      // 如果节点只有一个子节点。
      // 获取子节点。
      /** @var BinarySearchTreeNode */
      const childNode = nodeToRemove.left || nodeToRemove.right;
      // 如果节点有父节点，则将子节点替换为当前节点的父节点的直接子节点。
      if (parent) {
        parent.replaceChild(nodeToRemove, childNode);
      } else {
        // 否则，用子节点替换要删除的节点。
        BinaryTreeNode.copyNode(childNode, nodeToRemove);
      }
    }

    // 清除被移除节点的父节点。
    nodeToRemove.parent = null;

    return true;
  }

  /**
   * 查找最小值节点
   * @return {BinarySearchTreeNode}
   */
  findMin() {
    // 如果没有左子节点，说明当前节点就是最小值节点。
    if (!this.left) {
      return this;
    }
    // 递归调用左子节点的findMin方法，直到找到最小值节点。
    return this.left.findMin();
  }
}

BinarySearchTree

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
export default class BinarySearchTree {
  /**
   * 初始化方法
   * @param {function} [nodeValueCompareFunction]
   */
  // 创建一个构造函数，它接受一个可选的 `nodeValueCompareFunction` 参数
  constructor(nodeValueCompareFunction) {
    // 创建一个新的 `BinarySearchTreeNode` 对象，值为 `null`，并使用提供的 `nodeValueCompareFunction` 作为比较器。
    this.root = new BinarySearchTreeNode(null, nodeValueCompareFunction);

    // 从根节点中获取节点比较器。
    // 将 `root` 节点的 `nodeComparator` 属性赋值给当前实例的 `nodeComparator` 属性。
    this.nodeComparator = this.root.nodeComparator;
  }

  /**
   * 插入值
   * @param {*} value
   * @return {BinarySearchTreeNode}
   */
  insert(value) {
    return this.root.insert(value);
  }

  /**
   * 判断是否包含值
   * @param {*} value
   * @return {boolean}
   */
  contains(value) {
    return this.root.contains(value);
  }

  /**
   * 移除值
   * @param {*} value
   * @return {boolean}
   */
  remove(value) {
    return this.root.remove(value);
  }

  /**
   * 对象的字符串方法
   * @return {string}
   */
  toString() {
    return this.root.toString();
  }
}